The Decibel (dB) Scale & Audio Rules 101

For those looking to gain a deeper understanding of how audio works, whether to make better-informed decisions or simply for the sake of curiosity, it's useful to lay down some ground rules that govern how audio systems behave relating to loudness and the decibel.

One of the most important concepts in audio is the decibel, the unit of measure denoting the ratio of a change in level, whether that level is acoustic Sound Pressure Level (SPL) or electrical signal level. It’s abbreviated dB. As you may or may not be aware, the decibel (dB) scale is a logarithmic system, as opposed to a linear scale. Being aware of the relationships inherent in this scale is important for a variety of reasons, which will hopefully become clear by the time you reach the end of this article.

Rule #1:  +3dB = 2x the amplifier power; +10dB = 10x the amplifier power

Going from 1 watt to 2 watts of amplifier power gains 3dB of additional output; that's a pretty good deal right? Again, going from 2 watts of amplifier power to 4 watts gains an additional 3dB of output. Given the relatively low cost of amplifier power these days, buying a more powerful amplifier is a no-brainer.

So now that we have a basic understanding of the relationship between watts and SPL, let's complicate things a bit: What if there is a significant price difference between an 80 watt amplifier and a 100 watt amplifier? Things can get a little hazy here. Manufacturers do have their ways of skewing their wattage ratings, so the first thing you need to do is make sure you are comparing apples to apples. In other words, the amplifier power ratings must be rated under the same conditions.

A manufacturer may choose to rate it the “old fashioned” way, per the 1974 FTC power amplifier rating requirements, which came into being at that time in order to do away with all the misleading and vague ratings schemes like IHF Power, Music Power, IPP Power, etc. The FTC standard required that amplifier manufacturers state their output wattage over a specific frequency range (usually 20-20kHz, for mid- and high-end units), at a stated level of % Total Harmonic Distortion (THD), with both channels driven simultaneously, into a stated load impedance (4 or 8 or 16 ohms) after a one-hour preconditioning period at 33% power. It was a great standard. Unfortunately, it was never upgraded to take multi-channel home theater receivers or powered subwoofers or self-contained computer speakers and docking stations into account.

These days, in the era of multi-channel home theater receivers, the “both channels driven simultaneously” requirement has been mostly disregarded. Some of the ‘better’ brands will rate their 5- or 7-channel receiver in “2-channel mode” per the 1974 specs, but then they give a vague optimistic rating for multi-channel operation. Worse yet, the FTC has abandoned any effort to bring specificity and accountability to power ratings, so the consumer is really on their own when trying to compare the output specs from different brands.

Example:  Receiver ‘A’ may state “120 watts x 7 @ 1kHz .5% THD, 8 ohms,” but then in really small print say, “65 watts continuous x 2, 20-20kHz, .1% THD 8 or 4 ohms.”

Receiver ‘B’ may state, “90 watts x 7 @ 1 kHz, .3% THD, 6 ohms,”, but not give a 2-channel 20-20k rating at all.

Good luck comparing those. Actually, it’s quite plausible, given the way the power is spec’d here, that these two units have absolutely identical output capabilities!

You can read more on this topic with our article Product Managing Receiver Platforms .  

Nonetheless, all else being equal (say, an incremental jump in a specific manufacturers lineup), aside from 100 watts having a nice ring to it, the “extra” 20 watts of power represents a rather insignificant 1dB step.

What about a 200 watt amplifier versus a 400 watt amplifier? In an ideal world, and again all else being equal, you'd be looking at another 3dB gain. There are some obstacles about going to 400 watts, however, as most speakers can’t handle that kind of power.

There are three broad categories as to why speakers can only handle a certain power level:

1. Thermal. Power is hot! Excessive power will heat voice coils to the point where they can expand and bind up in the voice coil gap; heat can deform VC formers, soften adhesives, burn crossover resistors, all kinds of things. Speakers can tolerate some thermal abuse for short periods, but if too much heat builds up for too long, the speaker will suffer a thermal-related failure….commonly called “burn out.”
2. Mechanical. Excessive power input will demand that the speaker’s drivers try to move long distances, perhaps farther than they were designed to. This can cause the driver’s voice coil to “jump the gap,” or move so far that the voice coil comes out of the gap, misaligns, and can’t return to its original position. That’s an excessive power-caused mechanical failure.
3. Magnetic/Compression. This happens when the power input is so great that the speaker’s magnetic structure saturates and can’t convert the input signal into additional mechanical energy A speaker is a transducer—a device that converts one form of energy (electrical) into another (mechanical/acoustic)— and at this point, it stops “transducing.” At these extreme power levels, the speaker actually puts out a softer signal. This is known as compression, because the speaker compresses its output in response to a greater input signal.

Here is a useful table of a real-world situation with two low-to-medium efficiency speakers in a normal listening room and a listening distance of about 9 feet.

Let’s say you have a speaker with a sensitivity rating of 86dB 1m on-axis with a 2.83V input. Some might consider 86 dB to be on the “low” side for sensitivity.

But 86dB is really a pretty healthy level, much more than background listening. It may not be loud enough in a dealer showroom, but in your quiet listening room, you’d have to turn it down to answer the phone.

Now, you’ve got two speakers, so there’s some addition to the 86 SPL figure because of that. You are also about 8-10 feet away from the two speakers (and somewhat off axis, to boot), so there’s some reduction because of that (the inverse square law, which says that SPL reduces by -6 dB as the distance doubles). Throw in your room’s absorptive characteristics, any open walls that lead to the next room, etc, and what you’re left with is that the raw sensitivity figure for one speaker is a pretty decent number to work with as to how loud two speakers will sound from your listening position with a 2.83V (1 watt into 8 ohms, 2 watts into 4 ohms) input. There are a LOT of variables, obviously, but 86dB for 1 watt per speaker for a pair of speakers from your listening chair is not a bad estimate.

Editorial Note about Inverse Square Law & Real Rooms

We’ve all heard the -6dB inverse square law of SPL reduction for every doubling of distance but in reality that pertains to free space, or an anechoic chamber – which is a room without echoes.  Real world listening rooms will see more along the lines of 3-4dB of loss for every doubling of distance.  But for arguments sake, we stick to the common -6dB figure for all of our calculations in this article.  Just recognize the real world losses should be much less, unless of course you live in an anechoic chamber or are listening to your speakers outdoor in free space. 

Every doubling of power is another +3dB of loudness. So:

2 w = 89 dB

4 w = 92 dB

8 w = 95 dB

16 w = 98 dB

32 w = 101 dB

64 w = 104 dB

128 w = 107 dB

256 w = 110 dB

As you can see, even relatively modest amplifiers can drive these speakers to healthy loudness levels in a normal room.

The need for power escalates very quickly as you approach “lifelike” or “theater” levels of around 100-104 dB. Likewise, an average loud listening level of, say, 91 dB punctuated by a sudden peak of 10-20 dB will make a huge instantaneous demand on your amplifier. This is where your amp can run out of steam very quickly. That logarithmic loudness-watts scale we spoke about earlier really comes into play here.

So what should you, the avid reader, learn from all this?

Ultimately, there are two takeaways:

a. More power is usually never a bad thing, but eventually you will reach a point of diminishing returns when limited speaker capability, rising amplifier cost, and situational listening limitations (you’re in an apartment, for instance, and 105 dB peaks are simply not possible in your world) conspire together to put an upper limit on your amplifier power usage.

Interesting side discussion: There is a commonly held position among knowledgeable audiophiles that says speakers—especially tweeters—are more often damaged by lower-powered amplifiers than higher-powered amplifiers. The reasoning goes like this: in order to get higher SPLs, lower-powered amps are often turned up to the point that they put out a distorted signal. Since THD distortion products are whole-number multiples (“harmonics,” hence the “H” in the term Total Harmonic Distortion) of the fundamental frequency, at higher frequencies like 5 kHz or 8 kHz, the 2^nd harmonic distortion product will be 10 kHz or 16 kHz—barely audible as stand-alone test tones, never mind when they’re buried in the mix of an actual ‘busy’ musical signal. But if the amplifier is putting out substantial distortion due to “clipping” (being driven into severe distortion such that its output waveform appears “clipped” when viewed on an oscilloscope), then the tweeter is being fed a very high level of ultrasonic energy, and they suffer thermal failure, even though the HF distortion may not be that audible to the user.

This is why higher-powered amplifiers are said to be ‘safer’ than low-powered amps, because high power amps are far less likely to be pushed to the point of clipping and thus do not send high levels of ultrasonic (but inaudible) energy to the tweeter.

On the opposite side of this issue are such notable engineers like Ken Kantor of AR and NHT fame. They dismiss this theory entirely, saying that pure high levels of power—even so-called “clean” power— are the primary danger to speakers. Excessive heat is excessive heat, whether it’s delivered by a distorted or undistorted signal, and excessive heat is what burns out a tweeter’s fragile voice coil.

b. Don't fret small differences in amplifier power. All else being equal, you're not going to notice a big difference between an 80 watt amplifier and a 100 watt amplifier, except perhaps in your pocketbook.

Manufacturers often increase the functionality and flexibility of the feature set as they move up from one model to the next. The power ratings are often rounded into nice, “comfortable” numbers, so they make  sense from a marketing standpoint. If model “A” is 75 watts x 7, then model “B” with 2-zone capability, more HDMI inputs, better digital decoding circuitry, and a logical step to a nice round “100 watt” x 7 rating gives models A and B a legitimate reason to co-exist in the lineup.

As an example, the Onkyo TX-NR717 at $949 versus $649 for the next step down TX-NR616, are fairly logically priced, with power ratings and feature sets that seem perfectly commensurate with their asking price. Just be aware that in the real world, 80 and 100 watts (of similar amplifier design) will sound virtually identical. But if you absolutely must have that additional HDMI input, it’s priceless, no?

Rule #2:  +6dB = double the sound pressure, 2x driver excursion

This statement has a lot of important implications. Certainly the notion that 6dB of extra output requires double the driver excursion (all else being equal for sealed systems; vented designs are a bit harder to generalize about) should give some appreciation for what it takes to achieve higher output levels. For example, if you have a pair of subwoofers in an open field (above the ground, away from any major reflective surface), also known as full space or 4π steradians (a full sphere), and you stack them one on top of the other or put them shoulder to shoulder, you will theoretically net a gain of 6dB versus running just a single subwoofer.

If you put that single subwoofer so its front radiating panel is flush with the wall (1/2 space or 2π steradians), you can also theoretically net a 6 dB gain. Back in the 1960’s, AR discovered that if they took their speakers outside and buried them in the ground with their front baffles flush with the ground and then close mic’ed the woofer’s LF response, they’d get extremely accurate 2π measurements.

If you take that subwoofer and place it at the floor/wall intersection, then that’s called a ¼ space or π, and you’ll gain another 6 dB of output reinforcement.

Finally, if you put that single subwoofer in a corner at the intersection of three room boundaries (1/8 space or ½ π), you can theoretically net a 18dB gain relative to the subwoofer out in the open field, above the ground. Where is all this apparently “free” output coming from one might ask? If you consider that a subwoofer is radiating energy in all directions (bass is omni-directional in its perceived output, as opposed to higher frequencies, which become more and more “flashlight-beam” directional as the frequency increases), the answer should become clear: out in an open field, much of a subwoofer's output is wasted as it isn't being reflected back on you, the listener. Boundaries help to focus that energy where it's needed, thus boosting apparent output. Of course, it is worth keeping in mind that in the real world, drywall and wooden stud construction doesn't make a "perfect" boundary, so the actual gains tend to be less than theory predicts.

Nonetheless, the takeaway is this: Giving the subwoofer some “help” by placing it near reinforcing room boundaries will increase its output without needing additional amplifier power and without requiring greater excursion (and hence getting more distortion) from the woofer.

A final thought for this section: by now you should be getting a good idea of what it takes to push the limits of performance: lots of amplifier power and a robust driver to turn that into acoustic output. It may seem a fool’s errand to chase a few more dB when the cost seems to go up out of proportion to the benefit: after all, in terms of dollars per dB, a subwoofer like the SVS PB12-NSD would appear to have a much better cost to benefit ratio than the PB12-Plus. To address this, we’ll need to discuss human perceptions with respect to the dB scale, which is coming up shortly. However, going back to the above formula just remember: a 6dB gain equates to double the pressure, and when we’re talking bass, we’re talking about frequencies we can feel as well as hear. Food for thought.

The SVS PB12-Plus. At under twice the price of the PB12-NSD, it delivers on average 6dB more clean output relative to its little brother, i.e. twice the sound pressure. Combined with its superior feature set, the value becomes a little more apparent. But what do our ears make of this? 

Rule #3:  Drop an octave = 4x the excursion (for sealed systems) to maintain output; comparable to an increase of 12dB

Awareness of the above is perhaps the biggest argument I can think of in favor of bass management. Consider that a single 5.25" driver in a sealed box needs roughly 1/2 inch of peak to peak throw to achieve 100dB of output at one meter at 80Hz. That's quite a lot of driver excursion, and also a good argument for something a bit meatier than a small bookshelf speaker if you're aiming for reference levels, which demand peaks of up to 105dB from each channel, as measured from the listening position. Now imagine expecting that poor 5.25" driver to reproduce 20Hz signals, which can be the case if you choose to run it full range. You'll need 8 inches of peak-to-peak excursion to maintain your 100dB output (16 times your 1/2 inch excursion at 80Hz for a drop of 2 octaves); in other words, it isn't going to happen.

This relationship is also interesting from the perspective that it should give you some appreciation for what it takes to dig down deep. Once you start approaching the infrasonic realm, even a few Hz can represent a big leap with respect to the octave scale, and consequently the requirements from a subwoofer to reproduce such low frequencies with authority. To put it another way: 10Hz to 20Hz is a mere 10 Hertz, but it is a full octave, as is 10 kilohertz to 20 kilohertz, even though that’s 10,000 Hertz difference. Octaves are 2:1. That’s what counts. A subwoofer designed to dig down to 20Hz with authority (Warp engines and exploding Death Stars, well below the musical range) will make a subwoofer designed to reach down to 32Hz (the lower limit of music, i.e. low “C” on a large pipe organ) look wimpy in comparison. 

The TC Sounds LMS Ultra 5400. For deep bass reproduction, there is no replacement for displacement, and an 18” driver with 33mm of Xmax has a lot of it!

A Word on Human Perception of Loudness

By now, your head may be spinning with numbers, and it’s time to bring it all home:

It’s great that 10 times the amplifier power can potentially yield an additional 10dB of output, but what does all this mean to you, the listener?  The answer is that it depends: our ears are complicated mechanisms whose sensitivity varies with frequency, and it is important to remember that you can feel as well as hear some sounds.

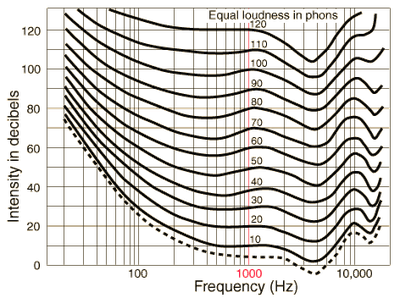
To start, it is worth taking a look at an equal loudness curve. You’ll notice that the threshold of hearing varies by frequency (it takes a large amount of acoustic output for us to hear a 20Hz tone, relative to 1kHz for example), and if you study the curves closely, you’ll being to see how the ear perceives jumps in SPL. At 1kHz, a 10dB gain correlates with a perceived doubling of loudness in some frequency ranges. As you go down in frequency, however, you’ll find that the lines start to compress together: Instead of needing a 10dB gain to double perceived volume, you will need roughly 4-5dB in the deep bass frequencies. Further, remembering that we feel as well as hear deep bass, and taking into account that a 6dB gain corresponds with a doubling of acoustic pressure, one may better appreciate the previous example of the SVS PB12-Plus versus the PB12-NSD.

For further reading on human hearing:

Human Hearing: How we Perceive Sound Summary Report

For information regarding safe SPL levels, and protecting your hearing:

Tip of the Day: Protect Your Hearing

A handy SPL calculator, as well as a chart equating dB levels with various real world examples:

SPL Calculator: How Loud will it get?

Conclusion

We hope that reading this article has given you clearer new perspective on the role and definition of “dB” and “loudness” in audio. It can indeed be a confusing subject, especially for those used to thinking in a linear scale. On the face of it, who would expect the difference between an 80 watt amplifier and a 100 watt amplifier to be insignificant in the real world? Who would imagine that upgrading to a subwoofer with a mere 6dB more output could be so important in the perception of bass “impact”? Well, now that you've read this article, you do. If you use this knowledge properly, it will help you make more effective purchasing decisions and also aid you in setting up your system. Happy listening!