Skin Effect Relevance in Speaker Cables
Some so called "exotic" Cable Companies enjoy spreading the fallacy that Skin Effect can cause deleterious effects on your audio performance. While Skin Effect is a real world problem in high frequency applications such as RF Power and Transmission, it is negligible at audio frequencies as I will demonstrate in this article based on fundamental engineering and scientific principles.
It is a good idea to brush up on speaker cable resistance before diving deeper into the topic of Skin Effect and AC resistance.
Skin Effect Defined
Skin Effect has been known and equations derived for skin depth vs frequency as far back as 1915. It is the tendency of alternating current to flow near the surface of a conductor, thereby restricting the current to a small part of the total cross-sectional area and increasing the resistance to the flow of current.
Note: The skin effect is caused by the self-inductance of the conductor, which causes an increase in the inductive reactance at high frequencies, thus forcing the carriers, i.e., electrons, toward the surface of the conductor. At high frequencies, the circumference is the preferred criterion for predicting resistance than is the cross-sectional area. The depth of penetration of current can be very small compared to the diameter.
Skin Depth
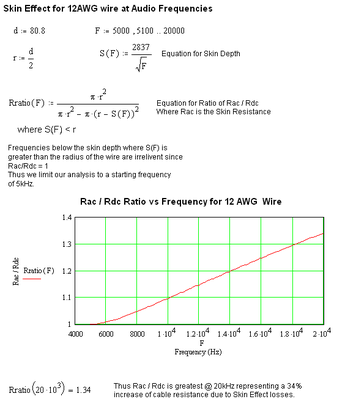
Skin Depth is defined as the distance below the surface where the current density has fallen to 1/e or 37% of its value at the surface. Because of Skin Effect, the AC to DC resistance of round wire is dependent on the ratio of the wire diameter to skin depth as can be seen in the equation below:
Rratio = Rac/Rdc = (pi*r^2) / (pi*r^2 - pi(r-S)^2)
where S < r ;
S = 2837 / sqrt(f) (Skin Depth)
(This equation has been derived by many sources and for copper wire at 70 degrees C, the above relationship holds true)
Note: This is a worst case calculation as cable resistance increases with temperature and most people will not be listening to music in a 70 degree C environment as they would probably be more occupied by trying to cool down or get out of such a heated room!
Further, since skin depth is inversely proportional to the square root of frequency, different size wires will have different AC to DC ratios, and these ratios will increase with frequency.
First lets make some basic assumptions for a high fidelity two channel audio set-up:
- Speaker Cables Length: 10ft / ea
- Speaker Cable Gauge: 12AWG round multi stranded OFC wire
Known Variables
- Diameter of 12AWG wire = 80.8 mils
- Maximum Audio Frequency (F) of Concern 20kHz (limit of human hearing)
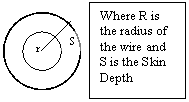
Illustrated below is the cross sectional area of 12 AWG wire showing the radius of the wire (r) and skin depth (S).
Note: Multi stranded 12 AWG wire cross sectional area is slightly larger than equivalent gauge solid core wire, thus we shall model our wire as solid core for a more conservative calculation as depicted in the figure below. As you may recall my elementry Algebra, the Area of a circle = pi*r^2.
Update: This is a very conservative calculation for increase in AC resistance due to skin effect because it assumes the current density profile is uniform within the first skin depth. This equation also assumes solid core wire which will exhibit higher skin effect compared to a similar gauge stranded wire. Further study shall be reserved on this topic for a later article.
Actual measured increase in AC Resistance due to Skin Effect at 20 kHz is less than 3%. See the results in our Cable Face Off Article for more details.
Skin Effect in Speaker Cables Calculations
The Skin Effect was calculated on the last page and simulated in MathCad to be:
Rac = 1.34 * Rdc @ 20kHz (worst case frequency)
For 12AWG wire the Rdc is about 1.6 ohms/1000 feet. (Source: Belden Cables )
For 10ft of cable, we get a Rdc of: (1.6 / 1000)*20 = 32 mohms.
Thus total Rcable Resistance (Rac) @ 20kHz = 1.34*32 = 42.9 mohms .
As you recall, we calculated that Skin Effect does attribute about a 34% increase in cable resistance at 20kHz. This again assumes solid core wire. In actuality, multistranded wire has less of an issue with skin effect because each individual strand has a smaller cross sectional area than the skin depth at the particular frequency. Although un-insulated multi stranded wire is not considered true Litz wire, it still behaves somewhat as such and thus reduces the overall skin effect problem. However, for argument sake we will ignore this factor and thus we will ultimately yield a more conservate estimate of the skin effect problem. Recall that actual measured increase in AC resistance at 20kHz due to skin effect was only about 3% from our Cable Face Off article.
But what does this mean in terms of real world losses?
First we have to make some additional basic assumptions. For it we fail to identify all of the important variables, while not eliminating the non essentials ones, we set ourselves up for defeat and the situation becomes hopelessly complex and too convoluted to accurately analyze.
Speaker Load Considerations
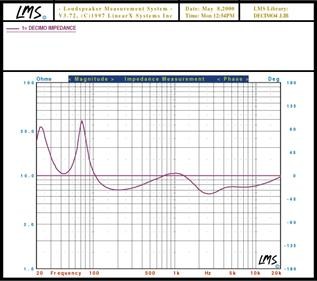
Ok, here is the tricky part. Since loudspeakers are reactive loads, and there are a wide assortment of products on the market all with their own individual impedance characteristics, we have to make some assumptions. Usually a good loudspeaker design maintains a stable impedance vs frequency within the audio band. Here is a plot from a loudspeaker previously reviewed on Audioholics.com.
As you can see, the magnitude of impedance is centered around the nominal impedance rating of the speaker (8ohms), with dips down to 6ohms.
This speaker load is a relatively easy load for an amplifier to drive. Most modern day loudspeakers are relatively benign loads to drive compared to some of the more difficult ESL designs which typically have impedance dips down to about an ohm at 20kHz. We consider the ESL case an outlier as it is not representitive of a typical consumer product and usually requires cabling with low DC resistance and inductance for optimal performance.
Lets take a worst case typical modern speaker design load and assume we have a dip down to 2 ohms at 20kHz (very rare case).
We can now determine the voltage divider ratio between the speaker cable and load.
Rcable = 42.9 mohms @ 20kHz
Rspeaker (magnitude) = 2ohms @ 20kHz
Loss(dB) = 20*log ( Rspeaker / (Rspeaker + Rcable) ) = -0.18dB loss.
Again, recall our measured increase of AC Resistance due to skin effect was only about 3% at 20kHz resulting in a total cable resistance of 32.96 mohms for a 10ft length.
Actual Measured Loss
Loss(dB) (act) = -0.142dB
As you can see, the resultant calculated loss due to Rdc and Skin Effect (Rac) in the cable is negligable. In fact, if we neglected the Skin Effect losses, the resultant loss would be -0.14dB just from the DC Resistance of the speaker cables alone.
Thus the calculated Skin Effect losses in this example only account for -.04dB of total loss at 20kHz while the measured Skin Effect losses would be a mere 0.002dB! Also don't forget this is assuming a 2 ohm load, which most modern speakers do not dip down that low at 20kHz. In reality, a real world speaker load would make this loss almost immeasurable.
Skin Effect in Speaker Cables - Conclusion
So What Does This All Mean In The Grand Scheme of Things?
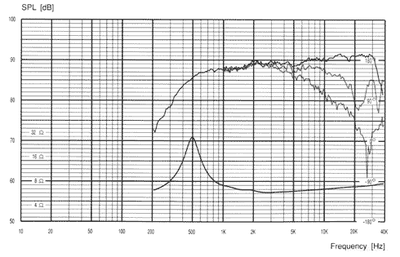
We know from our calculations that our total loss in a 10 foot run of 12AWG wire from the DC and AC resistances into a 2 ohm speaker load is -0.18dB at 20 kHz while our actual measured losses were -0.14dB. To get an idea for how insignificant this is in the grand scheme of things, I have included a frequency response plot from one of the industrys best dome tweeters which is known for its excellent dynamics, power handling, and on/off axis frequency response. Pictured below is the on and off axis (30, 60 degrees, respectively) of the Scan Speak 970000 or more popularly referred to by Audiophiles as the "Revelator".
Notice how this tweeter has a relatively flat frequency response to 20kHz, but falls off more than -10dB at 30° off axis at 20kHz, and -15dB at 60° off axis at 20kHz!
In the majority of two channel audio set-up's the listener does not listen to their speakers directly on-axis. Depending on the loudspeaker design, room acoustics, and listening preferences, the user may decide to slightly "toe-in" their speakers. However, even "toe-in" will not account for the majority of these losses. Since we don't listen to music in an Anechoic Chamber, room acoustics alone will further worsen this problem of high frequency attenuation.
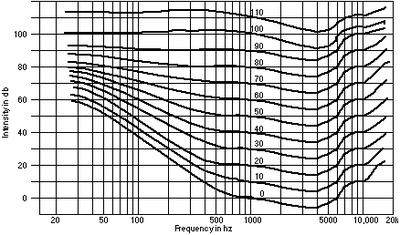
Fletcher & Munson Curve (Equal Loudness Contours)
We must also consider a very obvious, but often overlooked limitation to high frequency performance in our audio systems. Our Ears! The majority of adults can rarely hear up to 20kHz and those who are fortunate enough to hear up to 20kHz do so at a much less perceived level as can be seen by the Fletcher Munson curve that illustrates the sensitivty of human hearing related to amplitude and frequency response. Let us also not forget that there is hardly any musical energy that extends nearly up to 20KHz, as it is mostly harmonic in nature with very little applied power and thus resultant SPL at the loudspeaker.
This curve depects human perception of equal loudness vs frequency and amplitude. Notice the curve 50dB @ 1kHz; In order for the human ear to perceive 20kHz at the same loudness, the amplitude needs to be increased by 20dB to a total level of 70B!
So next time someone tries to tell you that their cables will reduce "Skin Effect" and thus will yield better high frequency performance or phase coherence of your system, smirk and ask them how they can reduce high frequency off-axis losses and minimze phase coherence problems of your loudspeakers, room acoustics losses resulting in associated phasing issues, human hearing sensitivity losses at high frequencies, and phase changes due to the changes of air pressure and soundwave propagation in your room?
Bottom Line
The bottom line is Skin Effect is not a relevant factor of concern when choosing / designing high performance loudspeaker cables for hifi audio systems. The DC resistance and inductance of the cable are far more important factors as can be seen in our Speaker Cable Face Off and Cross Coax vs Zip Cord articles where we modeled lumped element parameters (R,L,C) of speaker cables.
For more information on skin effect and its impact on cable resistance and inductance, see Calculating Inductance of Speaker Cables.
You should question the validity and intentions of a particular cable vendor(s) when they boast in their marketing literature about solving the "Skin Effect" problem, and ask yourself, "Are they stressing this point as a means to an ends to justify their outlandish asking price of their 'exotic' speaker cables"?
Next we will look at the Fallacy of "Strand Jumping" leading to the myth of diode rectification and how this theory cannot be sound as it violates basic Electrical Engineering Principles, the Laws of Physics, and common sense.
References
Belden Cables
"Switching Power Supply Systems" by Abraham I. Pressman , Second Edition