Physics Tutorial 1: Coulomb's Law & Electrostatics
Atoms are composed of three particles with an electric charge: electrons, protons and uncharged neutrons. Electrons have a negative charge, and protons have a positive charge. The negative charge of the electron has the same magnitude, or amount of charge, as the positive charge of the proton.
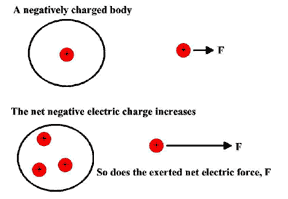
Electrical charge is quantized, with the smallest unit of electrical charge found in a single electron or proton. If we double the number of electrons or protons, we double the amount of negative or positive electric charge. If we triple the electrons or protons, we triple the electric charge. By increasing the amount of single unit electric charges, we have a net charge. A net charge is the summed value of single electrical charges.
We don't typically refer to single units of charge. We typically refer to net charges. Atoms are composed of protons and electrons and generally have a net neutral electrical charge. The magnitude of total positive and total negative charges inside the neutral atom is equal. If we were to remove an electron (called a Valence electron) from the atom, the net charge of the atom would be positive. There is now more positive charge in the atom. This atom is called a positive ion, and is quantized with a net positive charge.
What happens when we keep removing Valence electrons from a group of neutral atoms? We end up with a group of positive ions and a group of free Valence electrons. Each group has a net positive or net negative electrical charge. We can call each charged group a body of charge.
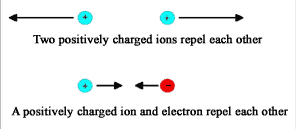
We can't really say what an electrical charge is, but only describe its behavior. Simply stated, two single protons or two single electrons repel each other. A single proton and a single electron attract each other. The same can be said for net charges - a net negative charge will attract a net positive charge.
This attracting and repelling action exerted on single electron or proton or a net electric charge is an electric force. Electric force is represented by vectors, which point in the direction the force is acting. The length of the vector represents the magnitude (the amount) of the electric force.
Several electrical charges can exert an electric force on a single electron, proton or a net electrical charge. When this occurs, there are several electric force vectors acting on the electrical charge. Vectors can be summed together to form a net vector. The electric force vectors can be summed together for a net electric force.
Remember and digest this-electrostatics is a description of the interaction of electric charges at rest in a frame of reference. In an electrostatic model, the net electric force on any electrical charge is zero, and therefore the electrical charge does not move. If you pushed a physics book lying on a table, the book would move in the direction you pushed it-there is a net force greater than zero acting on the book. If you did not push the physics book, the book remains still (static) and the net force on the book is zero . Electric current and activity in electric circuits occurs because of a net electric force greater than zero-the electric charges are forced into motion. Since electric current is electric charges in motion, it is not electrostatic and will be discussed in a later tutorial.
Note: Believe it or not, the table exerts a "normal" force back on the physics book. The normal force is equal to the weight of the book, but acts in the opposite direction. The forces are equal but opposite, and so they sum to zero. Don't believe me? I challenge you to look it up.
Electric charges attract and repel because of electric force. In the 18th century, Charles Augustin de Coulomb set up an experiment using the early version of what we call a Torsion Balance to observe how charged pith balls reacted to each other. These pith balls represented point charges; point charges are charged bodies that are very small when compared to the distance between them. Coulomb observed two behaviors about electric force:
- The magnitude of electric force between two point charges is directly proportional to the product of the charges.
- The magnitude of the electric force between two point charges is inversely proportional to the square of the distance between them.
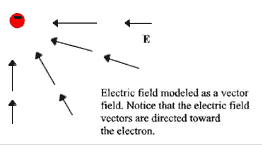
Let's build on our description of electrical interaction and electric force. For electric charges to cause an effect on other electric charges, physicists say that any electric charge somehow modifies the properties of the space around itself. The electric charge causes an electric field at some point in space. This electric field is present at that point in space, even if there is no other electrical charge at that point. Like the electric force, the electric field can be modeled with vectors, E.
The electric field can vary from every point in space around the electric charge, so it is not a single vector quantity. Electric field is an infinite set of vectors, each vector associated with a point in space.
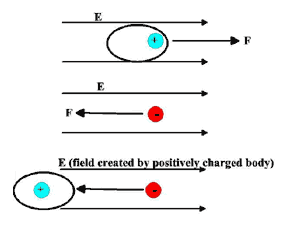
We model an electric field so that it is directed away from a positive electric charge that generated the field, and the electric field is directed towards a negative electric charge that generated it (the field).
Another negative electric charge inside the generated electric field would experience an electric force in the opposite direction of the electric field, regardless if the field is generated by a positive or negative charge. A positive electric charge in the generated electric field will experience an electric force in the same direction as the electric field. It's another way of demonstrating attraction and repulsion of electric charges!
There is a relationship between electric field, E , and the electric force, F , exerted on another electric charge in that field. The simplest mathematical description is the following expression:
F = q E
The symbol q represents the electric charge; q will be negative or positive depending on the electric charge. The vector E is positive or negative depending on the direction it is pointing-towards or away from the field generating electric charge.
Physics Tutorial 1: Gauss's Law & Conclusion
Gauss's Law
Gauss's law is an alternative to Coulomb's law for describing the relationship between electric charge and electric field. Gauss's law can be modeled using an imaginary closed surface, referred to as a Gaussian surface. This model even helps us in understanding electromagnetism, which will be covered in a later tutorial.
First, we start by completely enclosing an electric charge with an imaginary surface or imaginary box. Let's pretend this box has no effect on the electric field produced by the electric charge enclosed inside. Then, we look at the electric field at different points on this imaginary surface.
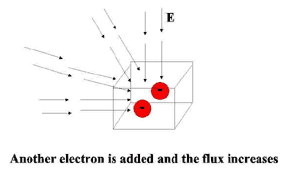
Since we now know that an electric charge produces an electric field, we could map out a three-dimensional electric field outside the box. Since there is a negative charge inside the box, the electric field would point toward the charge and into the box.
If there had been a positive charge inside the box, the electric field would point out of the box. This electric field mapping is called flux. Flux can be thought of as a flow into or out of the imaginary box, even though an electric field does not actually flow.
Now we place another negative electric charge inside the imaginary box. The amount, or magnitude, of the negative charge would increase and so does the flux.
What happens if a negative charge and positive charge of the same magnitude are enclosed in the box? Both generate electric fields, one into the box and one out of the box, so that the net flux (net flow) is zero. Will charges outside the box give a net flux through the box? No, because the flux will flow through one half of the box and flow out the other half.
There are two things you should note about flux, or the net flow through the Gaussian surface.
- The net flow of electric field through the Gaussian surface depends on the net amount of electric charge contained within the surface.
- The net flow through the surface is the product of the surface area and the component of electric field vector perpendicular to the surface. Think of it like a liquid flow- if the surface area was larger, more flux would flow into it and the net flux increases.
The above two points summarize Gauss's law. Gauss's law states that the total electric flux through a closed surface is proportional to the total electric charge enclosed within that surface. We can use this law to calculate fields caused by charge distributions with various symmetry properties. Gauss's law is valid for any distribution of charges and for any closed surface.
So what good is this Gauss's law, anyway? Let me give you an example. What if we were to place excess electric charge on a solid conductor that is at rest (electrostatic-no net motion of charge), and wanted to determine where those excess charges reside. Gauss's law tells us that the excess charge would reside entirely on the surface, and not in the interior of the conductor material. Remember- this is only true when the solid conductor is electrostatic, and there is no net electric charge motion (current) of the ions and valence electrons that make up the conductor.
Here's the proof. In an electrostatic situation the net effect of the electric field, E , at every point of the solid conductor must be zero, or there would be current flowing. Now create an imaginary Gaussian surface inside the solid conductor. Since the net effect of E is zero everywhere inside the conductor, Gauss's law tells us the net flow into the Gaussian surface must be zero and that there is no excess charge inside the Gaussian surface.
Now continue shrinking the Gaussian surface like a collapsing balloon until it encloses a region of the solid conductor so small we can call it a point inside the conductor. The electric charge at that point must be zero. We can do this over and over at any point inside the conductor, and always determine that there is no excess electric charge inside the solid conductor. Therefore, the excess electric charge must reside on the outside of the electrostatic conductor. Wow!
Summary
Tool One: Electrostatics and Coulomb's law
- An electric charge can be a single proton or electron, or a net electric charge, such as a group of free valence electrons in a conductor.
- The interaction is called an electric force, F .
- Electric force can be described as a single interaction, or a net result.
- Electrostatics is a description of interaction of electric charges at rest. Electric charge in motion is electric current. Electric current is in motion, and therefore is not electrostatic.
- Electric interaction can also be modeled as an electric field, E . The relationship between electric field, E , and electric force, F , can be characterized as
F = q E
- Coulumb's Law quantifies the interaction of electric charges at rest.
Tool Two: Gauss's law
- Gauss's law is an alternative to Coulomb's law for describing the relationship between electric charge and electric field
- Gauss's law simplifies the electric field model by representing it as a quantity of net flow or flux through an imaginary Gaussian surface.
- The net flow of electric field through the Gaussian surface depends on the net amount of electric charge contained within the surface.
- The net flow through the surface is the product of the surface area and the component of electric field vector perpendicular to the surface. Think of it like a liquid flow- if the surface area was larger, more flux would flow into it and the net flux increases.
- Gauss's law does indeed have practical applications