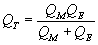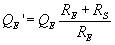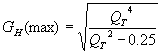“Let our rigorous testing and reviews be your guidelines to A/V equipment – not marketing slogans”

Damping Factor: Effects On System Response

by Dick Pierce — August 30, 2004

Much ballyhoo surrounds the concept of "damping factor." It's been suggested that it accounts for the alleged "dramatic differences" in sound between tube and solid state amplifiers. The claim is made (and partially cloaked in some physical reality) that a low source resistance aids in controlling the motion of the cone at resonance and elsewhere, for example:

"reducing the output impedance of an amplifier and thereby increasing its damping factor will draw more energy from the loudspeaker driver as it is oscillating under its own inertial power."

This is certainly true, to a point. But many of the claims made, especially for the need for triple-digit damping factors, are not based in any reality, be it theoretical, engineering, or acoustical. This same person even suggested:

"a damping factor of 5, ..., grossly changes the time/amplitude envelope of bass notes, for instance. ... the note will start sluggishly and continue to increase in volume for a considerable amount of time, perhaps a second and a half."

Damping Factor: A Summary
What is damping factor? Simply stated, it is the ratio between the nominal load impedance (typically 8W ) and the source impedance of the amplifier. Note that all modern amplifiers (with some extremely rare exceptions) are, essentially, voltage sources, whose output impedance is very low. That means their output voltage is independent, over a wide range, of load impedance.

Many manufacturers trumpet their high damping factors (some claim figures in the hundreds or thousands) as a figure of some importance, hinting strongly that those amplifiers with lower damping factors are decidedly inferior as a result. Historically, this started in the late '60's and early '70's with the widespread availability of solid state output stages in amplifiers, where the effects of high plate resistance and output transformer windings traditionally found in tube amplifiers could be avoided.

Is damping factor important? Maybe. We'll set out to do an analysis of what effect damping factor has on what most proponents claim is the most significant property: controlling the motion of the speaker where it is at its highest, resonance.

The subject of damping factor and its effects on loudspeaker response is not some black art or magic science, or even excessively complex as to prevent its grasp by anyone with a reasonable grasp of high-school level math. It has been exhaustively dealt with by Thiele and Small and many others decades ago.

System Q and Damping Factor
The definitive measurement of such motion is a concept called 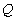. Technically, it is the ratio of the motional impedance to losses at resonance. It is a figure of merit that is intimately connected to the response of the system in both the frequency and the time domains. A loudspeaker system's response at cutoff is determined by the system's total 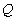, designated 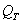, and represents the total resistive losses in the system. Two loss components make up 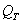: the combined mechanical and acoustical losses, designated by 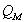, and the electrical losses, designated by 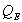. The total 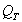is related to each of these components as follows:

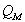is determined by the losses in the driver suspension, absorption losses in the enclosure, leakage losses, and so on. 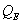is determined by the combination of the electrical resistance from the DC resistance of the voice coil winding, lead resistance, crossover components, and amplifier source resistance. Thus, it is the electrical 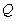, , 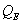that is affected by the amplifier source resistance, and thus damping factor.

The effect of source resistance on 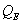is simple and straightforward. From Small(3):

where 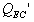is the new electrical 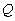with the effect of source resistance, 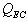is the electrical 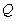assuming 0W source resistance (infinite damping factor), 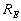is the voice coil DC resistance, and 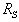is the combined source resistance.

It's very important at this point to note two points. First, in nearly every loudspeaker system, and certainly in every loudspeaker system that has nay pretenses of high-fidelity, the majority of the losses are electrical in nature, usually by a factor of 3 to 1 or greater. Secondly, of those electrical losses, the largest part, by far, is the DC resistance of the voice coil.

Now, once we know the new 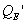due to non-zero source resistances, we can then recalculate the total system 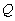as needed using eq. 2, above.

The effect of the total 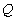on response at resonance is also fairly straightforward. Again, from Small, we find:

This is valid for 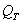values greater than 0.707. Below that, the system response is over-damped and there is no response peak.

We can also calculated how long it takes for the system to damp itself out under these various conditions. The scope of this article precludes a detailed description of the method, but the figures we'll look at later on are based on both simulations and measurements of real systems, and the resulting decay times are based on well-established principles of the audibility of reverberation times at the frequencies of interest.

Practical Effects of Damping Factor on System Response
With this information in hand, we can now set out to examine what the exact effect of source resistance and damping factor are on real loudspeaker systems. Let's take an example of a closed-box, acoustic suspension system, one that has been optimized for an amplifier with an infinite damping factor. This system, let's say, has a system resonance of 40 Hz and a system 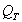of 0.707 which leads to a maximally flat response with no peak at system resonance. The mechanical 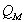of such a system is typically about 3, we'll take that for our model. Rearranging Eq. 1 to derive the electrical 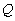of the system, we find that the electrical 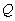of the system, with an infinite damping factor, is 0.925. The DC resistance of the voice coil is typical at about 6.5 W . From this data and the equations above, let's generate a table that shows the effects of progressively lower damping factors on the system performance

Damping factor	R _S	Q _E '	Q _T '	G _H(MAX)	Decay time
¥	0 W	0.925	0.707	0.0 dB	0.04 sec
2000	0.004	0.926	0.707	0.0	0.04
1000	0.008	0.926	0.708	0.0	0.04
500	0.016	0.927	0.708	0.0001	0.04
200	0.04	0.931	0.71	0.0004	0.04
100	0.08	0.936	0.714	0.0015	0.04
50	0.16	0.948	0.72	0.0058	0.04
20	0.4	0.982	0.74	0.033	0.041
10	0.8	1.04	0.77	0.11	0.043
5	1.6	1.15	0.83	0.35	0.047
2	4	1.49	0.99	1.24	0.056
1	8	2.06	1.22	2.54	0.069

The first column is the damping factor using a nominal 8W load. The second is the effective amplifier source resistance that yields that damping factor. The third column is the resulting 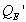caused by the non-zero source resistance, the fourth is the new total system 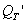that results. The fifth column is the resulting peak that is the direct result of the loss of damping control because of the non-zero source resistance, and the last column is the decay time to below audibility in seconds.

Damping Factor: Effects On System Response - page 2

Analysis

Several things are apparent from this table. First and foremost, any notion of severe overhang or extended "time amplitude envelopes) resulting from low damping factors simple does not exist. We see, at most, a doubling of decay time (this doubling is true no matter what criteria is selected for decay time). The figure we see here of 70 milliseconds is well over an order of magnitude lower than that suggested by one person, and this represents what I think we all agree is an absolute worst-case scenario of a damping factor of 1.

Secondly, the effects of this loss of damping on system frequency response is non-existent in most cases, and minimal in all but the worst case scenario. Using the criteria that 0.1 dB is the smallest audible peak, the data in the table suggests that any damping factor over 10 is going to result in inaudible differences between that and one equal to infinity. It's highly doubtful that a response peak of 1/3 dB is going to be identifiable reliably, thus extending the limit another factor of two lower to a damping factor of 5.

All this is well and good, but the argument suggesting that these minute changes may be audible suffers from even more fatal flaws. The differences that we see in figures up to the point where the damping factor is less than 10 are far less than the variations seen in normal driver-to-driver parameters in single-lot productions. Even those manufacturers who deliberately sort and match drivers are not likely to match a figure to better than 5%, and those numbers will swamp any differences in damping factor greater than 20.

Further, the performance of drivers and systems is dependent upon temperature, humidity and barometric pressure, and those environmental variables will introduce performance changes on the order of those presented by damping factors of 20 or less. And we have completely ignored the effects presented by the crossover and lead resistances, which will be a constant in any of these figures, and further diminish the effects of non-zero source resistance.

Frequency-Dependent Attenuation

The analysis thus far deals with one very specific and narrow aspect of the effects of non-zero source resistance: damping or the dissipation and control of energy stored in the mechanical resonance of loudspeakers. This is not to suggest that there is no effect due to amplifier output resistance.

Another mechanism that most certainly can have measurable and audible effects are response errors due to the frequency dependent impedance load presented by the speaker. The higher the output resistance of the source, the greater the magnitude of the response deviations. The attenuation can be approximated given the source resistance and impedance vs. frequency:

where is the gain or loss due to attenuation, is the amplifier source resistance, and is the frequency dependent loudspeaker impedance.

As a means of comparison, let's reexamine the effects of non-zero source resistance on a typical speaker whose impedance varies from a low of 6 ohms to a high of 40 ohms.

Damping factor	R _G	G _dB(MIN)	G _dB(MAX)	G _dB(ERROR)
¥	0 W	0 dB	0 dB	0 dB
2000	0.004	-0.006	-0.001	±0.003
1000	0.008	-0.012	-0.002	±0.005
500	0.016	-0.023	-0.003	±0.01
200	0.04	-0.058	-0.009	±0.025
100	0.08	-0.115	-0.017	±0.049
50	0.16	-0.229	-0.035	±0.098
20	0.4	-0.561	-0.086	±0.23
10	0.8	-1.087	-0.172	±0.46
5	1.6	-2.053	-0.341	±0.86
2	4	-4.437	-0.828	±1.8
1	8	-7.360	-1.584	±2.9

As before, the first column shows the nominal 8 ohm damping factor, the second shows the corresponding output resistance of the amplifier. The second and third columns show the minimum and maximum attenuation due to the amplifier's source resistance, and the last column illustrates the resulting deviation in the frequency response caused by the output resistance.

What can be seen from this analysis is that the frequency dependent attenuation due to the amplifier's output resistance is more significant than the effects on system damping. More importantly, these effects should not be confused with damping effects, as they represent two different mechanisms.

However, these data do not support the assertion often made for the advantages of extremely high damping factors. Even given, again, the very conservative argument that ±0.1 dB deviation in frequency response is audible, that still suggests that damping factors in excess of 50 will not lead to audible improvements, all else being equal. And, as before, these deviations must be considered in the context of normal response variations due to manufacturing tolerances and environmental changes.

Conclusions

There may be audible differences that are caused by non-zero source resistance. However, this analysis and any mode of measurement and listening demonstrates conclusively that it is not due to the changes in damping the motion of the cone at the point where it's at it's most uncontrolled: system resonances. Even considering the substantially larger response variations resulting from the non-flat impedance vs. frequency function of most loudspeakers, the magnitude of the problem simply is not what is claimed.

Rather, the people advocating the importance of high damping factors must look elsewhere for a culprit: motion control at resonance, or damping, simply fails to explain the claimed differences.

Appendix

The debate over damping factor is hardly a recent one. For example, the following letter appears in the August 1947 issue of Wireless World:

"In your April issue, D. T. N. Williamson refers to electromagnetic damping of a baffle-loaded loudspeaker, through low output resistance of the amplifier, as being important. I used to think so myself, and was the first to use the word 'damping factor' but my belief was much shaken by the following argument.

"If a loudspeaker can be represented by an equivalent circuit consisting of a resistance in series with an 'ideal' loudspeaker of 100 per cent efficiency, then the damping must be applied across the input terminals.

"In this case, even if the amplifier output resistance is zero, the damping is limited by the series resistance which, for 5 per cent efficiency, would be twenty times the resistance of the ideal loudspeaker. This extreme simplification, of course, leaves out the reactive components of the speaker impedance, but the argument still holds qualitatively.

"Can any reader of Wireless World point out any error in this argument? If it is true, there is very little gained by attempting to achieve excessively low output resistances."

F. Langford Smith,
Sydney, Australia
August 1947