Calculating Inductance of Speaker Cables
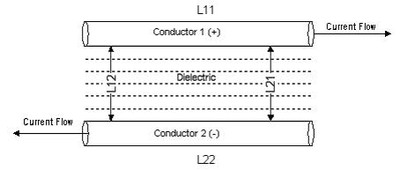
A typical Twin Feeder cable, or more popularly referred to as "Zip Cord", consists of two adjacent conductors separated by insulation, or commonly referred to a "dielectric". For convention we assume Conductor 1(+) current flows from left to right, and Conductor 2 (-) return current flows from right to left as illustrated below.
Listed below are the relationships of inductance for these types of cables.
Self Inductance: is comprised of internal and external inductances (L11 = Le1 + Li1, L22 = Le2 + Li2) Where the internal inductance of a straight wire with circular cross sectional area carrying a uniform low frequency current is 1.27 * 10^-3 uH/in or .0152 uH/ft. In the case of a Zip Cord speaker cable, the total internal inductance at or below audio frequencies is
2*(.0152) = .0304 uH/ft
Mutual Inductance: is a result of L1 and L2 interaction (L12) where L12 < Le2, and L2 and L1 interaction (L21) where L21 < Le1. The coupling coefficient (for two identical conductors) is equal to the Mutual Inductance divided by the Self Inductance where L12 / L11 = L21 / L22 .
If we neglect internal inductance and assume that the cable length is much greater than the conductor spacing:
K = [ ln (2*l / d)] / [ln (2* l / r)]
where l is he cable length, d is the conductor separation, and r is the conductor radius.
Total Inductance: Is the sum of Self Inductance and Mutual Inductance where:
Ltot1 = L11 - L12 and Ltot2 = L22 - L21
(The negative sign of the terms L12 and L21, is the result of current flowing in opposite directions on conductors 1 and 2.)Total Loop Inductance is the sum of Ltot1 and Ltot2 where:
LTOT = Ltot1 + Ltot2 = L11 - L12 + L22 - L21
At Low to Mid Frequencies:
LTOT = .281*Log(B/A) + Li1 + Li2 where Li1 + Li2 = .0304 uH/ft for Zip Cord.
And B is the space between two conductors and A is the Radius of each conductor. For very closely spaced conductors, the internal inductance terms may become important, especially at or below audio frequencies.
Note: It is extremely important to minimize B to minimize total cable inductance.
At High Frequencies
Skin effect forces current to surface of conductors, thus internal inductance becomes negligible and Self Inductance becomes equal to External Inductance:
LTOT = Le1 -L12 + Le2 - L21 = .281*Log(B/A)
Summary
At low to mid frequencies, for twin feeder cables, both internal and external inductance should be considered. As frequency increases, skin effect causes the internal inductance to become negligible, since the current is forced to the surface of the conductors. "The theory behind negligible inductance at high frequencies is within a wire carrying DC, there is a uniform current density profile. The magnetic flux within the wire is zero at the geometric center, and increases linearly in value as you move towards the surface of the wire. Outside the wire, the field drops off as 1/R. When a conductor is skinning heavily, as in RF, all the current has moved to the outside surface of the conductor. From the field equations, the field within an infinitely thin cylindrical sheet of current is zero. So, at infinite frequency, the internal portion of the wire has no field, hence, no energy stored, and no inductance. That is how the skin effect alters the internal inductance of the wire." (John Escallier)
Acknowledgements
I would like to thank my following colleagues for their thorough peer review of this article:
- John Escallier
- Henry Ott (http://www.hottconsultants.com/book.html)